Research
I’m interested in using topological data analysis to study topological objects in lattice models from statistical physics and particle physics. In particular, I use ideas from applied topology to develop data-driven tools to study these topological objects and phase transitions associated to them. By building up a methodology for using persistent homology with well-understood lattice models such as the XY model, and SU(2) lattice gauge theory, the hope is that eventually it can help our understanding of phenomena at the forefront of physics like the deconfinement phase transition in quantum chromodynamics (QCD).
Quantitative analysis of phase transitions in XY models
One of the major projects of my PhD was to develop a methodology for using persistent homology with 2D XY models. These models can display point-like topological defects such as vortices, antivortices, and line-like defects such as domain walls. I came up with a class of filtrations which capture these defects as persistent 1-dimensional holes.
To get a flavour of what the persistence of the XY model tells us, I wrote a small web app that can be found here. 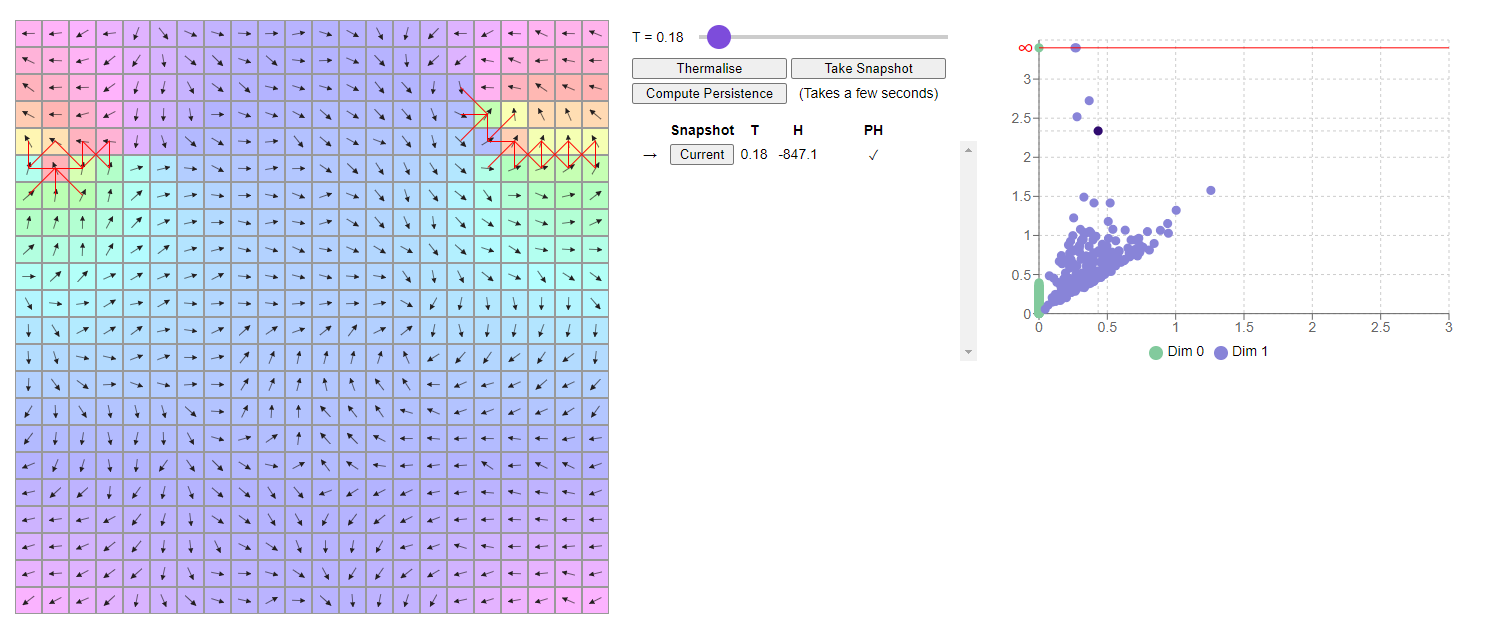
Beyond a qualitative picture of the vortices and antivortices of the XY model across the phase transition, the main aim was to obtain quantitative estimates of the transition temperature and one of the critical exponents of the transition. I achieved this using machine learning on persistence images demonstrating that, as you change the lattice size, the ML estimates of the transition temperature follow a certain scaling law. Besides allowing extrapolation of the continuum transition temperature and the critical exponent of correlation legnth, this provides evidence that the persistence is coupling to the degrees of freedom relevant to the phase transition. See the paper here.
Center vortices in SU(2) lattice gauge theory
My most recent project sought to detect vortices in configurations of SU(2) lattice gauge theory. We can think of this as being a toy model of QCD where the quarks are infinitely heavy and the gauge group is reduced from SU(3) to SU(2). Nevertheless, we're left with some of the interesting phenomena we're interested in such as confinement and the deconfinement phase transition. One of the most compelling arguments for why this transition occurs relies on objects called center vortices but, unlike the point-like vortices in the XY model, these take the form of two-dimensional closed surfaces. For a given configuration of the model, I defined a filtered complex complex that attempts to construct cubical approximations of those vortex surfaces based on the values of Wilson loops. In particular, the filtration is gauge-invariant where as most existing methods for looking at center vortices rely on gauge fixing. I demonstrated that the resulting persistence diagrams are sensitive to vortices that are explicitly inserted by boundary conditions, and that they can be used to quantitatively analyse the deconfinement phase transition. See the paper here.
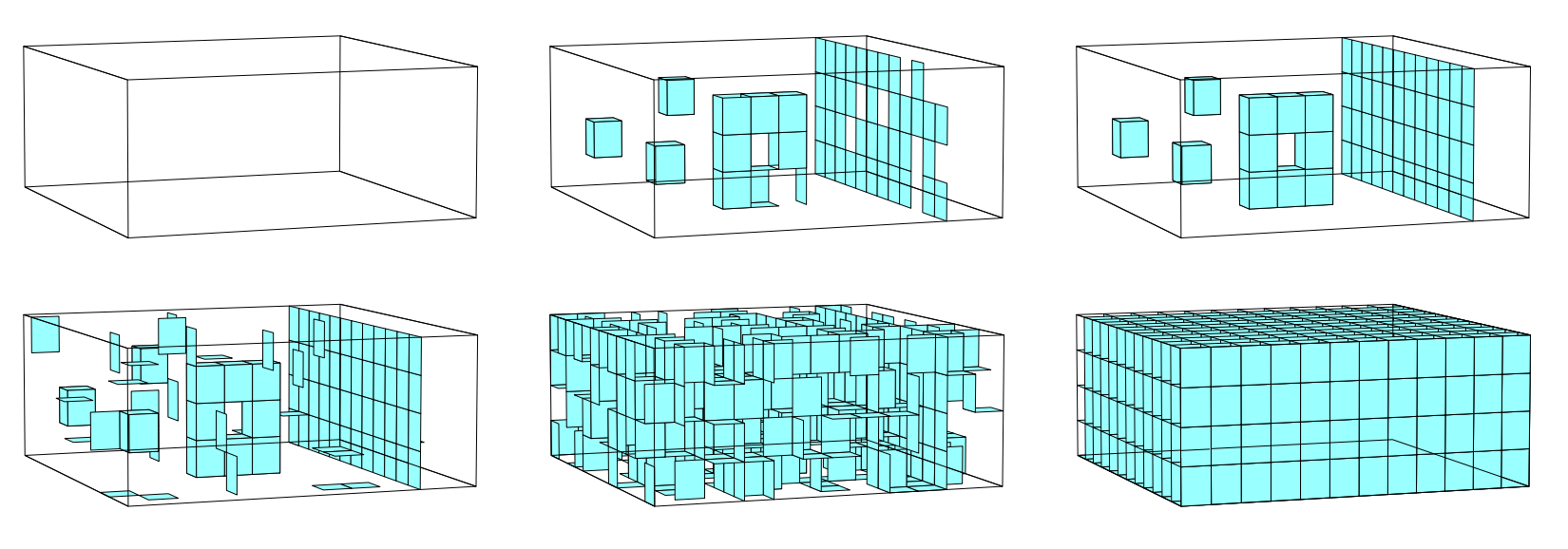
Other projects
In other previous projects I have looked at:
- varieties of polynomials in the triangle hyperfield with James Maxwell.
- developing non-parametric statistical tests for equality between distributions based on persistent homology.
Publications
with Jeff Giansiracusa and Biagio Lucini.
We investigate the use of persistent homology, a tool from topological data analysis, as a means to detect and quantitatively describe center vortices in SU(2) lattice gauge theory in a gauge-invariant manner. The sensitivity of our method to vortices in the deconfined phase is confirmed by using twisted boundary conditions which inspires the definition of a new phase indicator for the deconfinement phase transition. We also construct a phase indicator without reference to twisted boundary conditions using a simple k-nearest neighbours classifier. Finite-size scaling analyses of both persistence-based indicators yield accurate estimates of the critical β and critical exponent of correlation length ν of the deconfinement phase transition.
with Jeff Giansiracusa and Biagio Lucini.
We use persistent homology and persistence images as an observable of three different variants of the two-dimensional XY model in order to identify and study their phase transitions. We examine models with the classical XY action, a topological lattice action, and an action with an additional nematic term. In particular, we introduce a new way of computing the persistent homology of lattice spin model configurations and, by considering the fluctuations in the output of logistic regression and k-nearest neighbours models trained on persistence images, we develop a methodology to extract estimates of the critical temperature and the critical exponent of the correlation length. We put particular emphasis on finite-size scaling behaviour and producing estimates with quantifiable error. For each model we successfully identify its phase transition(s) and are able to get an accurate determination of the critical temperatures and critical exponents of the correlation length.
Proceedings
with Biagio Lucini and Jeff Giansiracusa.
Topological Data Analysis (TDA) is a field that leverages tools and ideas from algebraic topology to provide robust methods for analysing geometric and topological aspects of data. One of the principal tools of TDA, persistent homology, produces a quantitative description of how the connectivity and structure of data changes when viewed over a sequence of scales. We propose that this presents a means to directly probe topological objects in gauge theories. We present recent work on using persistent homology to detect center vortices in SU(2) lattice gauge theory configurations in a gauge-invariant manner. We introduce the basics of persistence, describe our construction, and demonstrate that the result is sensitive to vortices. Moreover we discuss how, with simple machine learning, one can use the resulting persistence to quantitatively analyse the deconfinement transition via finite-size scaling, providing evidence on the role of vortices in relation to confinement in Yang-Mills theories.
Theses
Submitted in August 2022. Download.
My masters dissertation, written over the course of Hilary Term 2019. It introduces homotopy type theory and looks at doing synthetic homotopy theory, focussing particularly on defining fibre bundles. The main result is a proof in homotopy type theory of a theorem originally due to Gottlieb. It gives the homotopy groups of the path components of the space $Map(X, K(G,1))$, where $X$ is any space and $K(G,1)$ is the classifying space of a discrete group $G$.
Submitted in April 2019. Download.
